Простейшие линейные уравнения

Простейшие линейные уравнения — это уравнения вида

   

где a и b — некоторые числа.

Чтобы решить линейное уравнение, надо обе части уравнения разделить на число, стоящее перед x:

   

Но делить на нуль нельзя. Поэтому линейные уравнения вида ox = b и ox =o решаются иначе.

Рассмотрим уравнение

   

Какое бы число мы не подставили в это уравнение вместо x, при умножении его на нуль в левой части получится нуль. А в правой — число, отличное от нуля. То нет значений x, при которых уравнение обратилось бы в верное числовое равенство. Значит, это уравнение не имеет корней.

   

Какое бы значение мы не подставили вместо x в данное уравнение, в левой части при умножении на нуль получится нуль. В правой части — также нуль. Значит,  решением данного линейного уравнения является любое число.

Таким образом, решение и количество корней линейного уравнения зависит от числа, стоящего перед x:

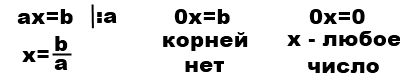
Замечание: 

Любое число можно разделить на 2, 5 и числа, которые можно представить только в виде произведения двоек и пятерок (например, 10=2∙5, 40=2∙2∙5). При делении на все остальные числа ответ записываем не в виде десятичной, а в виде обыкновенной дроби или смешанного числа.

Примеры простейших линейных уравнений:

1) 3x=-24

Это — линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом:

x=24:3

x=8.

Ответ: 8.

2) -7x=5

Это — линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом. Ответ записываем в виде обыкновенной дроби:

   

Ответ: -5/7.

3) 12y=20

Это — линейное уравнение. Обе части уравнения делим на число, стоящее перед y:

   

Сокращаем дробь на 4:

   

Получили неправильную дробь. Выделяем целую часть:

   

Ответ: 1  2/3.

4) 0x=8

Данное уравнение не имеет решений, поскольку при умножении на нуль любого числа в левой части получится нуль, а в правой — 8, то есть нет таких значений x, при которых уравнение обращается в верное числовое равенство.

Ответ: корней нет.