Определить, делится ли число на 4 нацело, можно с помощью признака делимости. Делимость на 4 зависит от двух последних цифр в записи числа.
1-й признак делимости на 4
Натуральное число делится без остатка на 4:
— если его запись оканчивается двумя цифрами, образующими число, которое делится на 4;
— если его запись оканчивается двумя нулями.
Чтобы не проверять делимость на 4 числа, образованного двумя последними цифрами, непосредственным делением, можно воспользоваться другим признаком.
2-й признак делимости на 4
Натуральное число делится без остатка на 4, если сумма предпоследней цифры в его записи и половины последней цифры — чётное число.
Схематически делимость на 4 трёхзначного числа в этом случае выглядит так:
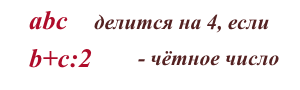
Для шестизначного числа признак делимости на 4 схематично можно изобразить так:

1) Определить, какие из данных чисел делятся без остатка на 4:
23452; 1400; 75415; 43928; 9672; 87530; 6497; 10000; 311020; 712112; 45908; 65439; 83760; 56736; 34514; 39782.
Решение:
Прежде всего отбросим все нечётные числа: 75415, 6497, 65439 — они не делятся на 4.
Далее отбираем числа, запись которых оканчивается двумя нулями: 1400, 10000 — они делятся на 4.
В оставшихся числах проверяем делимость на 4 числа, образованного двумя последними цифрами:
23452 делится на 4, так как 52 делится без остатка на 4 (5+2:2=5+1=6 — чётное число).
43928 делится на 4, так как 28 делится на 4.
9672 кратно 4, так как 72 кратно 4 (7+2:2=7+1 — чётное число).
311020 делится нацело на 4, так как 20 делится на 4.
712112 делится на 4, так как 12делится на 4.
45908 делится на 4, так как 08 делится на 4.
83760 делится на 4, так как 60 делится на 4 (6+0:2=6 — чётное число).
56736 делится на 4, так как 36 делится без остатка на 4.
87530 не делится на 4, так как30 не делится нацело на 4.
34514 не делится на 4, так как 14 не кратно 4.
39782 не делится на 4, так как 82 не делится без остатка на 4 (8+2:2=8+1=9 — нечётное число).
Ответ: 23452; 1400; 43928; 9672; 10000; 311020; 712112; 45908; 83760; 56736.
2) Найти какое-либо четырёхзначное натуральное число, кратное 4, сумма цифр которого на 1 больше их произведения.
Решение:
Самый простой случай — если запись натурального числа оканчивается двумя нулями. В этом случае произведение цифр числа равно нулю. Значит, сумма цифр должна равняться единице. Подходящий вариант — 1000.
Ответ: 1000.
