Типичные задачи на совместную работу в 6 классе
1) Двое рабочих, работая вместе, выполняют некоторую работу за 6 часов. Один из них, работая самостоятельно, может выполнить эту работу за 15 часов. За сколько часов может выполнить эту работу другой рабочий?
В отличие от всех других типов задач, задачи на совместную работу начинаются с того, что всю работу (все задание, весь бассейн, все поле — то, о чем идет речь в задаче) принимаем за единицу. То есть объем работы в этом случае равен единице. Чтобы найти объем работы, надо производительность труда умножить на время работы. Соответственно, чтобы найти производительность труда (часть работы, выполненную за определенную единицу времени), надо объем работы разделить на время работы: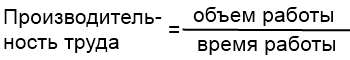 
Решение задач на совместную работу упрощается, если условие оформить в виде таблицы.
Перейдем с решению нашей задачи.
Решение.
Примем всю работу за 1.
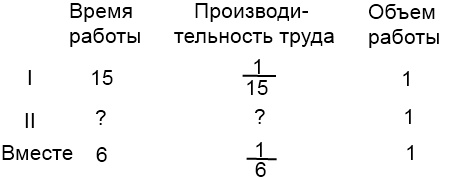
Чтобы найти производительность труда второго рабочего, из производительности труда совместной работы вычтем производительность труда первого рабочего:
![\[1)\frac{{{1^{\backslash 5}}}}{6} - {\frac{1}{{15}}^{\backslash 2}} = \frac{{5 - 2}}{{30}} = \frac{3}{{30}} = \frac{1}{{10}}\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-3dafc7a4fad5d07a77db59fb6f603e11_l3.png "Rendered by QuickLaTeX.com")
Такую часть работы в 1 час выполняет второй рабочий.
Зная производительность труда второго рабочего и объем работы, можем найти время, за которое он может выполнить работу самостоятельно. Чтобы найти время работы, надо объем работы разделить на производительность труда:
![\[2)1:\frac{1}{{10}} = 1 \cdot \frac{{10}}{1} = 10\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-f8d5dfcb78da59d0b99331e9b64b06c7_l3.png "Rendered by QuickLaTeX.com")
Значит, второй рабочий, работая отдельно, может выполнить работу за 10 часов.
Ответ: за 10 часов.
2) Через одну трубу бассейн наполняется за 7 часов, а через другую опустошается за 8 часов. За какое время бассейн будет наполнен, если открыть обе трубы?
Решение.
Примем весь бассейн за 1.
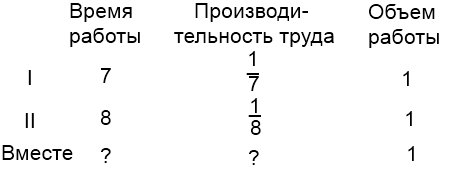
Сначала найдем производительность труда совместной работы обеих труб за один час. Поскольку одна труба бассейн наполняет, а другая — опустошает, производительность совместной работы равна разности производительности первой и второй труб:
![\[1)\frac{{{1^{\backslash 8}}}}{7} - \frac{{{1^{\backslash 7}}}}{8} = \frac{{8 - 7}}{{56}} = \frac{1}{{56}}\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-fb6fc97fe21dd470cfde939fd76dd32a_l3.png "Rendered by QuickLaTeX.com")
Теперь найдем время, за которое бассейн будет наполнен при открытии обеих труб одновременно. Чтобы найти время работы, надо объем работы разделить на производительность труда:
![\[2)1:\frac{1}{{56}} = 1 \cdot \frac{{56}}{1} = 56\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-2c60025746858da92919728ccfd63b9a_l3.png "Rendered by QuickLaTeX.com")
Таким образом, за 56 часов совместной работы обеих труб бассейн будет наполнен.
Ответ: за 56 часов.
Cпасибо за очень простые объяснения и понятные примеры!!!
Пожалуйста, Михаил! Успехов Вам в учебе!
Спасибо огромное!Смотрела на всех сайтах и только на вашем сайте нашла понятные объяснение!Миллион раз спасибо!
Анастасия, спасибо и Вам за теплые слова!
Спасибо огромное,помогло на экзамене
Данеля, я рада, что информация Вам пригодилась. Тем более приятно, что речь идет о таком серьезном мероприятии, как экзамен!
Спасибо большое ,вы мне очень помогли сдать экзамен!Спасибо!
Супер, нашел что хотел а то забыл как решать)
суперрррррр!!! а где еще?
«Еще» — это что? 🙂
Thank you so so so much!!! Amazing material! absolutely lovely — you saved me so much time — appreciate that.
Спасибо большое за хорошее объяснение задач на совместную работу!!!!!!!!!!!
Спасибо у меня экзамен,а я подзабыла как решать такие задачи.
Да, на ЕГЭ такие задачи встречаются.
Маша, удачи Вам на экзамене!
Супер. Классно объяснили все понятно.
Спасибо! Вчера контрольную сдал!
Молодец, Михаил!
Спaсибо очень огромное BAМ
Пожалуйста! 🙂
Огромное Вам спасибо. Очень все доступно и понятно. От таких объяснений ребёнок захотел решать задачи. Успехов Вам и здоровья. Спасибо.
Спасибо и Вам, Ольга, за теплые слова! Успехов Вашему ребенку в учёбе!
Спасибо очень помогли
Спасибо огромное!!! Очень всё просто и понятно!!! Вы мне очень помогли!!! Миллиард раз ОГРОМНЫХ ЧЕЛОВЕЧЕСКИХ БЛАГОДАРНОСТЕЙ И СПАСИБО!!!
Спасибо и Вам, Вика!
Спасибо вам!Я готовился к экзамену и в вашем сайте я вспомнил все!!!!!
Спасибо большое у меня такие задачи есть на экзамене.А есть задачи на масштаб?
Нет, задач на масштаб пока нет. Обещаю над этим поработать, но до Вашего экзамена не успею, увы.
Спасибо. Хорошее объяснение даже для 9 класса
как же такое может быть, что одна труба наполняет бассейн за 7 часов, а работая вместе за 56 часов????
Ирина, всё дело в том, что через вторую трубу вода при этом выливается.
Спасибо,Светлана,что ответили. Невнимательно прочитала задачу.Не подумала, что можно заполнять бассейн при сливе.
Спасибо от имени моей олимпиады по физике
Надеюсь, олимпиада была успешной для Вас)
Вторая задача не правильно решена. получается две трубы медленнее .чем одна наполнят бассейн?))
Да. Потому что через вторую трубу вода выливается.
Замечательный сайт , очень помогло , когда рассказывала учительница было не понятно , а сейчас раз и разобралась , спасибо огромное .
Спасибо и Вам, Таня, за тёплый отзыв! Когда читаю такую оценку, появляется желание продолжить работу над сайтом.
СПАСИБО ОГРОМНОЕ ! я теперь смог понять эти задачи !И спасибо за понятное обьяснение
Очень помогло
Спасибо большое за понятное объяснение! Вы нам очень помогли!
Спасибо Вам большое! Я делал домашку по математике и забыл, как решать такие задачи, буквально засыпал на уроке, а тут я быстренько прочитал и разобрался, спасибо ещё раз)
Максим, так приятно, когда ученики разбирают материал, а не ждут готового решения)
Спасибо огромное! Наконец-то разобралась!
Спасибо большое вам мне это очень помогло разобраться в теме ещё раз спасибо