Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз. Соответственно, при уменьшении одной из них в несколько раз, другая уменьшается во столько же раз.
Зависимость между такими величинами — прямая пропорциональная зависимость. Примеры прямой пропорциональной зависимости:
1) при постоянной скорости пройденный путь прямо пропорционально зависит от времени;
2) периметр квадрата и его сторона — прямо пропорциональные величины;
3) стоимость товара, купленного по одной цене, прямо пропорционально зависит от его количества.
Чтобы отличить прямую пропорциональную зависимость от обратной можно использовать пословицу: «Чем дальше в лес, тем больше дров».
Задачи на прямо пропорциональные величины удобно решать с помощью пропорции.
1) Для изготовления 10 деталей нужно 3,5 кг металла. Сколько металла пойдет на изготовление 12 таких деталей?
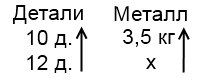
(Рассуждаем так:
1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
2. Чем больше деталей, тем больше металла нужно для их изготовления. Значит, это прямо пропорциональная зависимость.
3. Поэтому вторая стрелка одинаково направлена с первой).
Решение:
Пусть х кг металла нужно для изготовления 12 деталей. Составляем пропорцию (в направлении от начала стрелки к ее концу):
12:10=х:3,5
Чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член:
![\[x = \frac{{12 \cdot 3,5}}{{10}}\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-6f6a3185a50b9a197789ac3293a9caa9_l3.png "Rendered by QuickLaTeX.com")
![\[x = 4,2\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-0a37ec16b3c724850237bd3ee448d799_l3.png "Rendered by QuickLaTeX.com")
Значит, потребуется 4,2 кг металла.
Ответ: 4,2 кг.
2) За 15 метров ткани заплатили 1680 рублей. Сколько стоят 12 метров такой ткани?
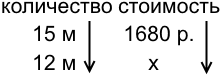
(1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
2. Чем меньше ткани покупают, тем меньше за нее надо заплатить. Значит, это прямо пропорциональная зависимость.
3. Поэтому вторая стрелка одинаково направлена с первой).
Решение:
Пусть х рублей стоят 12 метров ткани. Составляем пропорцию (от начала стрелки к ее концу):
15:12=1680:х
Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член пропорции:
![\[x = \frac{{12 \cdot \mathop {1680}\limits^{112} }}{{\mathop {15}\limits_1 }}\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-f02d05c933e909fa72e72e7fe4d3add0_l3.png "Rendered by QuickLaTeX.com")
![\[x = 1344\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-e889c1364dbd8b6d56c65d3cb1ede0fb_l3.png "Rendered by QuickLaTeX.com")
Значит, 12 метров стоят 1344 рубля.
Ответ: 1344 рубля.
Ничего не понимаю!! Фигня!
Пуся, сдаться — проще всего. Пробуйте разобраться.
Вы пишете во второй задаче,что стрелку ставим от большего числа к меньшему,а на самой картинке стрелки смотрят вверх-от меньшего к большему ?!?!?!
Да, Ната, стрелку следует ставить от большего к меньшему, сейчас так.
Просто условились ставить именно так, а могли договориться ставить иначе, от меньшего к большему.
Главное, что в задачах на прямо пропорциональную зависимость стрелки обязательно должны быть одинаково направленными, а на обратно пропорциональную зависимость — противоположно направленными.
ну,вроде бы поняла. в школе ужасно объсняют,спасибо)
Эти стрелки, вообще, никому НЕ НУЖНЫ. Они только запутывают учеников. Решать пропорцией. И ВСЕ! ЗАЧЕМ стрелки?!
Валентина, если бы с помощью пропорций решали только задачи на прямо пропорциональную зависимость, без стрелок вполне можно было бы обойтись. Но есть ещё и обратно пропорциональная зависимость, где без стрелок можно легко ошибиться. Они нужны, чтобы правильно составить пропорцию.
Спасибо вам Светлана Михайловна, объяснение и оправдание доказательств меня вполне устраивает, скажите вы учитель? Если нет, то жаль, я бы дала вам своего ребёнка на обучение. И да дети вы молодцы , что находите ошибки и все такое, но уважение к старшим должно быть!)
Здравствуйте, уважаемая мама гений! Последние 14 лет я работаю как репетитор, до этого 16 лет — в школе.
Спасибо, мои дети все поняли!)
Спасибо большое, всё понятно, легко справился с заданием. У учительницы было мало времени на нормальное объяснения, а это сильно помогло.