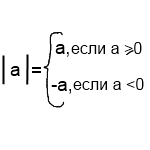Определение модуля | Математика для школьников

1. Определение модуля:

Модулем числа а называется расстояние (в единичных отрезках) от начала координат до точки А с координатой а.

Пример.

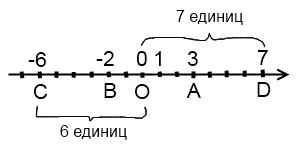
Модуль числа 7 равен 7, так как точка D с координатой 7 удалена от начала отсчета на 7 единичных отрезков.

Модуль числа -6 равен 6, так как точка С с координатой 6 удалена от начала отсчета на 6 единичных отрезков. Пишут:

$\left| 7 \right| = 7;\left| { - 6} \right| = 6$

2. По определению модуля, модуль — это расстояние.

А так как расстояние не может быть отрицательным числом, то и модуль не может быть отрицательным числом.

3. Модуль положительного числа равен самому числу.

Например,

$\left| {34} \right| = 34;\left| {7,8} \right| = 7,8;\left| {3\frac{5}{9}} \right| = 3\frac{5}{9}$

4. Модуль отрицательного числа равен противоположному числу.

Например,

$\left| { - 25} \right| = 25;\left| { - \frac{7}{{45}}} \right| = \frac{7}{{45}};\left| { - 2\frac{3}{{14}}} \right| = 2\frac{3}{{14}}$

5. Модуль нуля равен нулю:

$\left| 0 \right| = 0$

6. Противоположные числа имеют равные модули:

$\left| { - a} \right| = \left| a \right|$

Например,

$\left| { - 5} \right| = \left| 5 \right| = 5;\left| {\frac{4}{7}} \right| = \left| { - \frac{4}{7}} \right| = \frac{4}{7}$

Из определения модуля: