Здесь мы рассмотрим, что такое пропорция, как называются члены пропорции и основное свойство пропорции.
Определение пропорции:
Пропорция — это равенство двух отношений.
С помощью букв пропорцию записывают так:
![\[a:b = c:d\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-2989a14c8e6167dcd8afcc320213f3ea_l3.png "Rendered by QuickLaTeX.com")
или
![\[\frac{a}{b} = \frac{c}{d}\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-947c383783d4f9c72ec308b9b3863822_l3.png "Rendered by QuickLaTeX.com")
Читают: «a относится к b как c относится к d» или «отношение a к b равно отношению c к d».
Числа a и d называют крайними членами пропорции, числа b и c — средними членами пропорции:
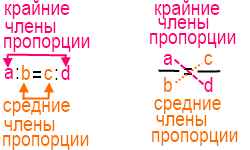
Примеры пропорций:
1) 4,8:1,6=3,6:1,2
Здесь 4,8 и 1,2 — крайние члены пропорции, 1,6 и 3,6 — средние члены пропорции.
![\[2)\frac{{2,1}}{{8,4}} = \frac{{1,5}}{6}\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-d3c87bfbef858213137904c41891687f_l3.png "Rendered by QuickLaTeX.com")
Здесь 2,1 и 6 — крайние члены пропорция, 8,4 и 1,5 — средние члены пропорции.
Основное свойство пропорции:
Произведение крайних членов пропорции равно произведению ее средних членов.
![\[a:b = c:d, \Rightarrow ad = bc\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-08fb585d0c73dc003ca509f799fa74ef_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{a}{b} = \frac{c}{d}, \Rightarrow ad = bc\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-57e0eb38329bb7710c2ea50c42d88999_l3.png "Rendered by QuickLaTeX.com")
Отсюда следует, что
![\[ad = bc, \Rightarrow \frac{c}{a} = \frac{d}{b};\frac{a}{c} = \frac{b}{d}.\]](http://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-bb147948dcd3f1555a4f6e5d738d868b_l3.png "Rendered by QuickLaTeX.com")
Таким образом, если в пропорции поменять местами крайние члены или средние члены, то получим новые верные пропорции.
Пропорция- это равенство. Если это равенство содержит переменную, значение которой надо найти, то оно является уравнением. Как решать пропорции, мы рассмотрим в следующий раз.
Кроме того, пропорции используются для решения некоторых задач. В частности, пропорции существенно облегчают решение задач на проценты. Позже мы рассмотрим также решение задач с помощью пропорций.
нормально
люблю этот сайт
🙂
Очень удобно.
Блин только закончил читать что такое отношения в математике, как же легко все это понимать!!! Эту тему я выучил за 1 час, а в школе бы учил неделю!!! Обожаю вас, спасибо за этот отличный сайт!!!!!!!!!!!
Спасибо! Но, думаю, и в школе можно выучить тему быстро, было бы желание.